Introducción

Este informe forma parte de una serie de reportes diarios que he venido realizando desde fines de marzo. La diferencia con los anteriores dice relación con un intento comparativo entre distintos momentos: antes y después del cambio que introduce el sinceramiento de 31.422 casos no reportados desde marzo hasta mediados de junio y que, a partir de esa fecha, comienzan a incorporarse. El objeto de este trabajo consiste en validar ciertos ajustes a la metodología que se venía empleando, a fin de continuar efectuando proyecciones que cuenten con un sustento real, puesto que resulta imposible incorporar esta ingente cantidad de casos no reportados en su oportunidad, dentro de las series históricas.

Para ello se acude a análisis anteriores al día 16 de junio, fecha de la modificación y, a la metodología empleada en ellos, se les introduce los mismos ajustes probados con posterioridad. Este análisis no tiene más pretensiones que la validación metodológica y evaluar el desempeño de cada modelo utilizado. Por ende, no aspira ni ha sido formulado en la perspectiva de un artículo de carácter académico.

En análisis anteriores se modelaban los enfermos activos, mediante un modelo epidemiológico, como así también los muertos. Lamentablemente, hubo que discontinuar estas proyecciones, debido a los cambios operados por el MINSAL en las metodologías de conteo, los cuales hicieron imposible los empalmes; primero fue la brusca e inexplicable caída de los infectados (de un día para otro descendieron de más de 60.000 a poco más de 20.000) y luego la incorporación de fallecidos no contabilizados con anterioridad.

Todos los análisis, desde marzo, se han basado estrictamente en las cifras oficiales de nuevos casos diarios del MINSAL, sobre las cuales se ensayan modelos matemáticos y se proyectan predicciones y escenarios. Desde este punto de vista, tampoco se persigue generar algoritmos que apunten hacia la inferencia de los contagios reales en el país, operando con la hipótesis de que los oficiales pudieren no responder a la realidad.

Los modelos presentados son univariantes, es decir, operan sobre la serie histórica de la variable de respuesta. Esta opción obedece a que no dispongo de información suficiente susceptible de incorporar para trabajar modelos más complejos o, incluso emplear métodos de Machine Learning.

En suma, el alcance de este trabajo, desde un principio, ha sido modesto y se ha limitado al ensayo de diversos modelos matemáticos –más allá de los tradicionalmente empleados en series temporales- procurando seleccionar aquellos que han ido obteniendo mejores desempeños en el tiempo, de acuerdo a las conductas que ha observado la pandemia. No apunta a desentrañar el cuadro real de la propagación del virus en Chile, ni a determinar el número real de contagiados en el presente o en el futuro, más allá de las cifras oficiales.

Como se señaló, hasta hace un tiempo se trabajaba también con un modelo epidemiológico (SIR simplificado que se cita en el anexo 1), sin embargo con el cambio de la modalidad de conteo de infectados y muertos, se optó por discontinuar su aplicación.

Como se consigna en el anexo 1, se ensayaron también modelos de transferencia con la población en cuarentena como variable exógena, con distintos lapsos de rezago, pero sin resultados significativos.

Evolución

En primer lugar, se examinará el comportamiento de la curva hasta el día de hoy, en términos generales, con el propósito de formarnos una primera idea sumaria acerca de la evolución del virus en el país.

La evolución de casos reportados –al día 113, que corresponde al 23 de junio- y que representa la totalidad de los casos, se presenta en el siguiente gráfico:

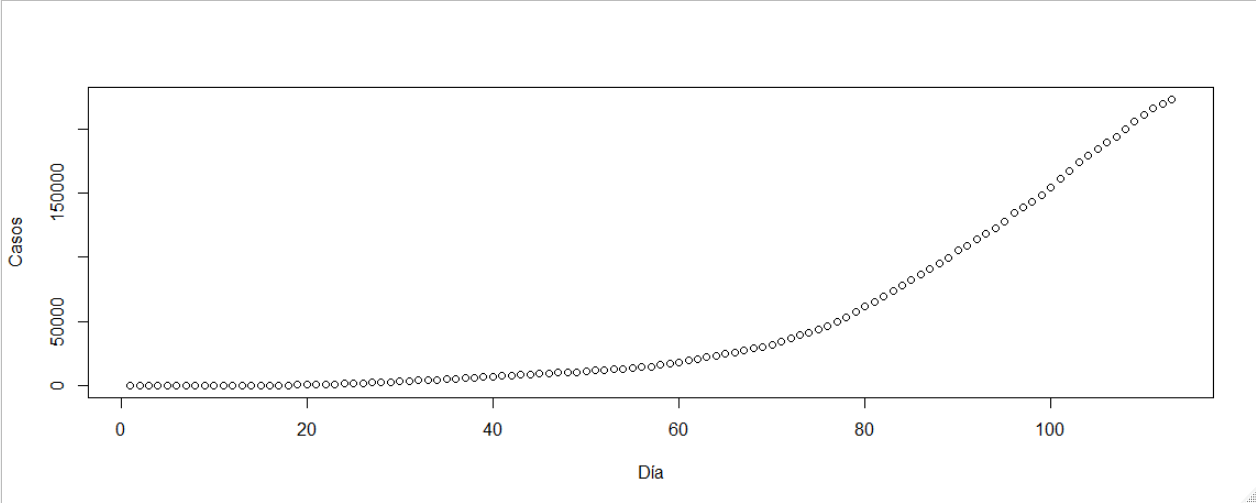
Es posible advertir diversas fases de evolución:

1. Los primeros 15 días aproximadamente, se conducen en la forma típica de evolución inicial de toda epidemia: una recta horizontal que despega mínimamente y que da cuenta de un incremento bajo y lento de los casos.
2. A partir del día 15, comienza a verificarse un efecto multiplicativo que dura hasta el día 22.
3. Desde el día 23 hasta más o menos el día 57, se consolida una recta con pendiente baja y estable; en estricto rigor de trata de tres rectas que exhiben leves aumentos de pendiente entre ellas, conforme avanza el tiempo.
4. El día 58 la curva experimenta un salto significativo (que corresponde a lo comentado al principio) y se vuelve a estabilizar otra recta con una pendiente bastante más pronunciada y que dura hasta el día 70.
5. A partir de del día 71, se produce un nuevo incremento significativo y se inicia una otra fase de efectos multiplicativos que se mantiene hasta el día 103.
6. De allí en adelante se verifica una suerte de estabilización de los nuevos casos, tendencia que, si se conecta hacia atrás desde los días 95-96, delinea un período estacionario.
7. Si bien no es riguroso extraer alguna conclusión, sí pareciera estarse confirmando el
   escenario del peak (más adelante se explicita qué se entiende por peak en este estudio) y el anuncio del el aplanamiento. No obstante, es prematuro aventurar pues la conducta de los últimos días podría ser parte de la fase estacionaria, con variaciones caprichosas.

De la observación del recorrido completo, se trata de una curva con efectos multiplicativos
en el tiempo y que, tomando en consideración la evolución de la epidemia en otros países,
podría estar adquiriendo un efecto de orden estacionario. De ser así, estaríamos viviendo el
escenario del peak desde la semana pasada (del 15 al 21 de junio) y se avizoraría el aplanamiento de la curva en los próximos días, tal como se había predicho en reportes de semanas anteriores.

A continuación, se muestra la evolución de la tasa diaria de nuevos casos reportados:

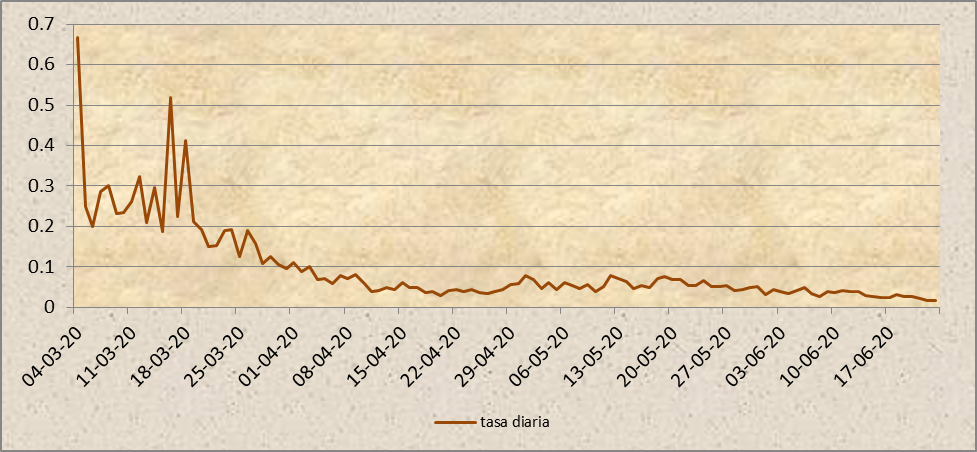
Se aprecia con nitidez cómo la tasa diaria disminuye en el tiempo. Desde el 18 hasta el 30 de abril se mantuvo estable sedimentando, sin embargo, a partir de ahí experimenta un alza importante que coincide con el cambio de fines de abril. Una tendencia hacia la baja comenzó a principios de junio y se observa una caída con una clara sedimentación, en los últimos diez días.

Desempeños de modelos matemáticos empleados

Se ensayaron muchos modelos distintos, desde el 20 de marzo aproximadamente. Aun cuando la curva no ha seguido nunca una conducta exponencial, sí en su recorrido se aprecian los efectos multiplicativos que la signan. En marzo se realizaron ensayos con modelamientos exponenciales y con distintos tipos de distribución, todos los cuales explotaban en los primeros días de abril; incluso se especificaron modelos exponenciales suavizados, con modelos aditivos, los cuales igual se disparaban en abril.[1]

En este acápite, se presentan los resultados de aquellos modelos con mejor desempeño en proyecciones de corto, mediano y largo plazo y que han sido consistentes en el tiempo. Esta presentación será comparativa, contrastando las proyecciones de hoy con aquellas anticipadas en semanas anteriores; y persigue, tal como se señaló, validar el nuevo camino metodológico adoptado, en virtud de la agregación de más de 31.000 casos no reportados durante todo el transcurso de la pandemia, junto con testear el poder predictivo de los modelos empleados.

A continuación, se exhiben algunas de estas proyecciones solamente a partir de fines de mayo (por razones de extensión y a modo de ilustración), realizadas con las metodologías que se venían empleando y corregidas por los ajustes que se aplican ahora, cotejándose con los datos reales.

 

día 89 (30 de mayo)	gampoisson	gampoli2	arima210	dato real	Modelos con mejor desempeño[2]
16-06-20	235175	212057	233297	220628
17-06-20	242354	217280	240694	225103
18-06-20	249658	222553	248241	231393
19-06-20	257086	227877	255936	236748	gampoli2
20-06-20	264638	233250	263778	242355
21-06-20	272315	238673	271766	246963
22-06-20	280116	244146	279897	250767
23-06-20	288041	249669	288172	254416
día 90 (31 de mayo)
16-06-20	232796	215487	248510	220628
17-06-20	239814	220900	257290	225103
18-06-20	246953	226366	266283	231393
19-06-20	254211	231883	275486	236748	gampoli2
20-06-20	261590	237452	284901	242355
21-06-20	269090	243073	294525	246963
22-06-20	276709	248746	304359	250767
23-06-20	284449	254471	314400	254416
día 92 (2 de junio)
16-06-20	224877	215164	217604	220628
17-06-20	231337	220563	223564	225103
18-06-20	237902	226013	229623	231393
19-06-20	244574	231515	235775	236748	arima210
20-06-20	251352	237068	242021	242355	gampoli2
21-06-20	258235	242674	248359	246963
22-06-20	265225	248330	254787	250767
23-06-20	272321	254039	261304	254416
día 93 (3 de junio)
16-06-20	221813	215645	224250	220628
17-06-20	228034	221078	230862	225103
18-06-20	234355	226564	237597	231393
19-06-20	240777	232102	244453	236748	gampoli2
20-06-20	247298	237692	251429	242355	gampoisson
21-06-20	253919	243334	258524	246963
22-06-20	260641	249027	265735	250767
23-06-20	267462	254773	273063	254416
día 95 (5 de junio)
16-06-20	216702	215426	220214	220628
17-06-20	222488	220857	226465	225103
18-06-20	228363	226340	232817	231393	gampoisson
19-06-20	234327	231875	239283	236748	gampoli2
20-06-20	240380	237461	245853	242355	arima210
21-06-20	246521	243100	252532	246963
22-06-20	252752	248790	259313	250767
23-06-20	259084	255427	267258	254416
día 97 (7 de junio)
16-06-20	216708	220272	225915	220628
17-06-20	222423	226113	232732	225103
18-06-20	228225	232011	239717	231393	gampoisson
19-06-20	234114	237963	246815	236748	gampoli2
20-06-20	240089	243972	254063	242355
21-06-20	246152	250036	261433	246963
22-06-20	252301	256156	268942	250767
23-06-20	259518	263569	274981	254416
día 98 (8 de junio)
16-06-20	215772	218834	210715	220628
17-06-20	221375	224564	215552	225103
18-06-20	227062	230348	220426	231393	gampoli2
19-06-20	232833	236186	225370	236748	gampoisson
20-06-20	238687	242079	230360	242355	arima210
21-06-20	244626	248027	235410	246963
22-06-20	250648	254029	240508	250767
23-06-20	256754	260086	245660	254416
día 100 (10 de junio)
16-06-20	216082	218748	222617	220628
17-06-20	221651	224484	229268	225103
18-06-20	227304	230275	236037	231393	gampoli2
19-06-20	233039	236120	242946	236748	gampoisson
20-06-20	238857	242020	249979	242355	arima210
21-06-20	244757	247975	257146	246963
22-06-20	250741	253984	264439	250767
23-06-20	256039	259750	268106	254416
día 102 (12 de junio)
16-06-20	218924	221975	227359	220628
17-06-20	224748	228125	234972	225103
18-06-20	230662	234334	242719	231393
19-06-20	236665	240601	250680	236748	gampoisson
20-06-20	242757	246927	258801	242355	gampoli2
21-06-20	248938	253312	267120	246963
22-06-20	255208	259755	275609	250767
23-06-20	261568	266256	284287	254416
día 104 (14 de junio)
16-06-20	221651	223841	223224	220628
17-06-20	227807	230321	229755	225103
18-06-20	234061	236863	235965	231393
19-06-20	240412	243467	242589	236748	gampoisson
20-06-20	246862	250132	249119	242355	arima210
21-06-20	253410	256859	255905	246963
22-06-20	260056	263648	262703	250767
23-06-20	266799	270499	269679	254416
día 105 (15 de junio)
16-06-20	221957	223043	221096	220628
17-06-20	228174	229384	226296	225103
18-06-20	234491	235786	231633	231393
19-06-20	240907	242248	236994	236748	arima210
20-06-20	247424	248770	242454	242355	gampoli2
21-06-20	254040	255353	247960	246963	gampoisson
22-06-20	260756	261997	253546	250767
23-06-20	267571	268701	259188	254416

 

Se consideran los modelos cuyos errores son inferiores al 5%.

Por lejos, el modelo de mejor comportamiento es el modelo aditivo polinomial cuadrático, el cual predice con gran exactitud las cifras de hoy desde fines de mayo. También cobra fuerza en los últimos días, ajustándose bien tanto frente a los incrementos como a los períodos estacionarios.

Se constata la potencia predictiva del gampoisson en el mediano y largo plazos, sin embargo en los últimos días –cuestión que se verá ratificada cuando se analicen las proyecciones de los días más inmediatos- este modelo comienza a perder su poder predictivo. Este fenómeno podría estar asociado a la inminencia del escenario del peak, dando cuenta de que posee un mejor rendimiento ante los efectos multiplicativos.

El arima (2,1,0) igual demuestra un buen poder predictivo, aunque evidencia problemas ante las variaciones muy bruscas; requiere que estos cambios alcancen cierto grado de estabilidad para recuperar su capacidad predictiva. En razón de ello, tal como se verá, se afirma más en los últimos días, sin cambios caprichosos y en fase estacionaria.

Resultados actuales y escenarios

Antes que todo, nuestro concepto de peak no alude al día que registra el mayor número de casos nuevos y que, a partir de ahí, dejarán de aumentar los casos nuevos reportados. Lo concebimos como aquel breve lapso de tiempo estacionario que opera como la inflexión que anuncia el denominado aplanamiento de la curva. Este concepto descrito es arbitrario y no necesariamente puede corresponderse con otros que pudieren tener una aceptación más universal en epidemiología; simplemente es una operacionalización lógica que interpreta la forma típica que adopta la curva logística –que describe la evolución de una epidemia- en su fase superior cuando adviene el aplanamiento asintótico. Sería la fase inmediatamente anterior, o la víspera, de la caída de los nuevos casos diarios. Con este concepto se trabajará, corresponda o no a otras concepciones de peak utilizadas en la jerga epidemiológica.

Si se asume que se está en presencia de un ciclo estacionario y de la sedimentación de la tasa de casos nuevos diarios, es plausible presumir que se ingresó a la fase peak la semana pasada (del 15 al 21 de junio), tal como se predijo en semanas anteriores- cuya conclusión daría inicio al aplanamiento de la curva. Por cierto, ello supone que no surgirán nuevos efectos multiplicativos.

De este modo, se abren tres escenarios futuros probables: momento estacionario inmerso en el período peak, momento estacionario que se mantendrá estabilizado mucho tiempo y momento estacionario que puede dar lugar a nuevos incrementos prontamente. Las señales predominantes apuntan a la primera opción: momento que preanuncia el inicio del aplanamiento, el cual es probable que sea lento.

Las proyecciones de los últimos días, que se efectúan a continuación, si bien capturan los efectos de estacionariedad, no asumen un eventual aplanamiento de la curva; razón por la cual las proyecciones mediano y largo plazos perderían vigencia si este fenómeno se produce en el corto plazo. Más bien responden a los otros dos escenarios señalados.

Día 109 (19 de junio)

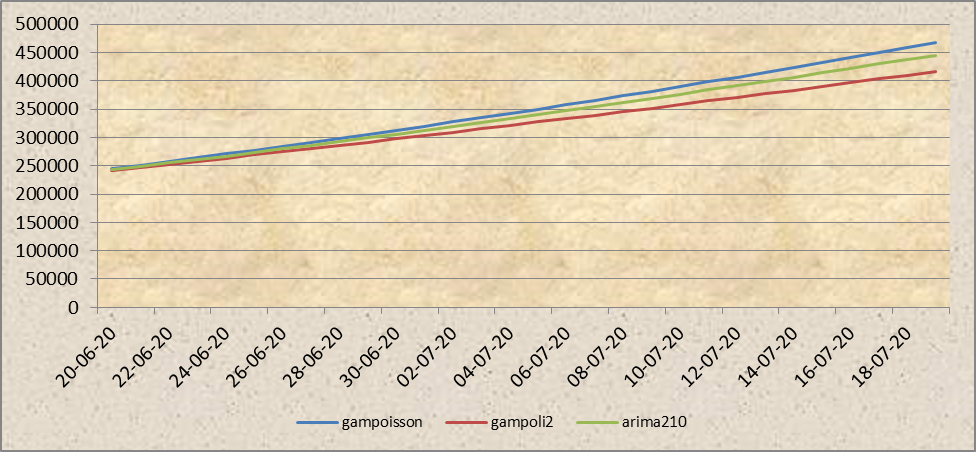
El modelo aditivo polinomial, comienza a acercarse al segundo escenario aunque con tenues incrementos, mientras que el modelo aditivo con distribución de Poisson recoge la posibilidad de nuevos efectos multiplicativos. Entretanto, el arima se sitúa en un punto intermedio.

Día 110 (20 de junio)

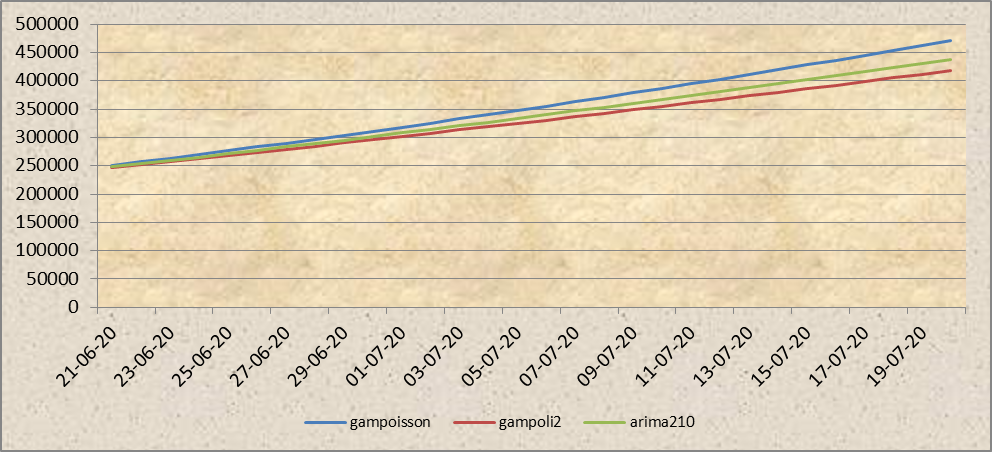
Se repite la condición anterior, aunque el arima se acerca más al modelo aditivo polinomial, en tanto el modelo aditivo con distribución de Poisson continúa reaccionando a la posibilidad de nuevos efectos multiplicativos.

Día 111 (21 de junio)

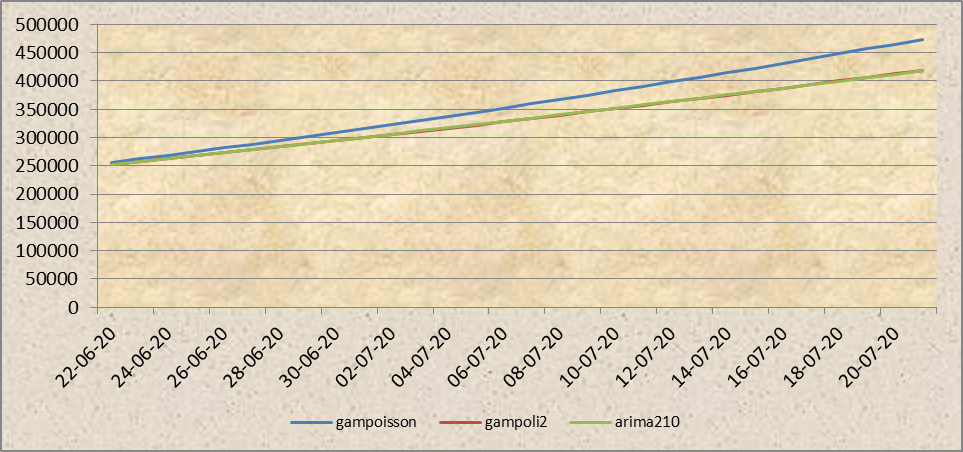
Definitivamente el modelo arima exhibe un comportamiento idéntico al polinomial cuadrático, haciéndose cargo del período estacionario con muy leves incrementos, mientras que el modelo aditivo con distribución de Poisson mantiene la conducta anterior.

Día 112 (22 de junio)

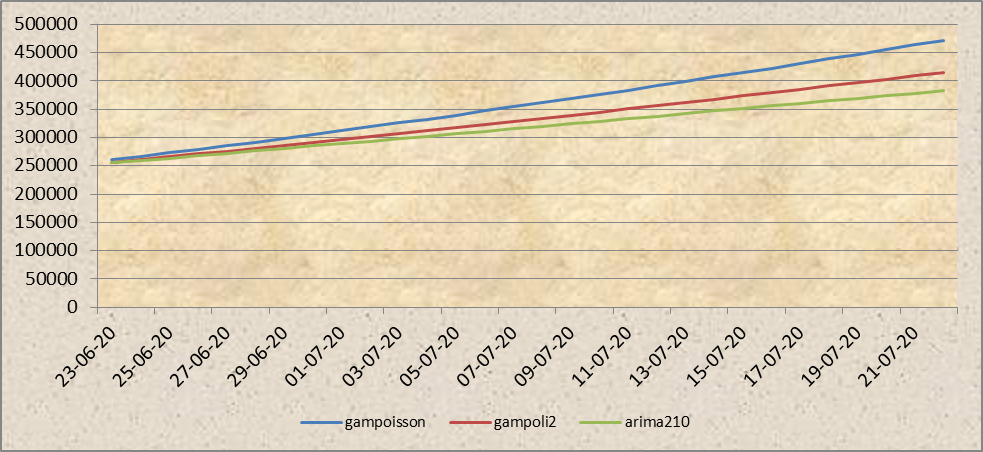
Esta vez se repite la tendencia de los días anteriores, con la diferencia que el arima comienza a hacerse cargo de la estacionariedad vigente. Destacamos que este modelo es sensible a las variaciones significativas.

Día 113 (23 de junio)

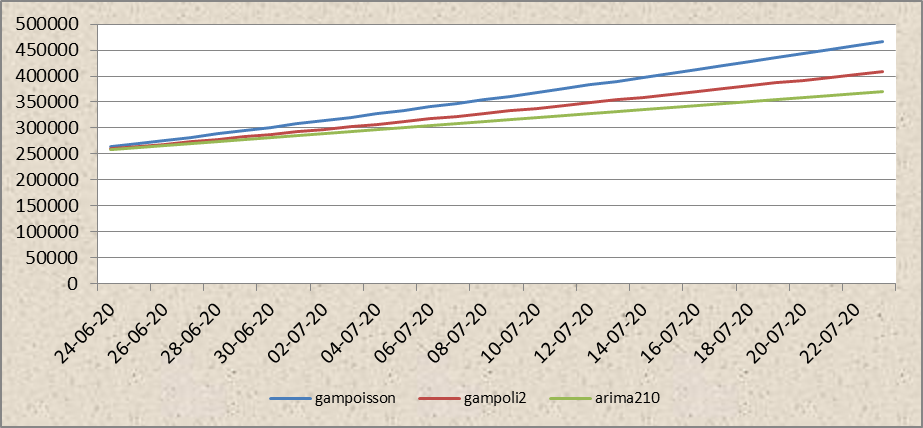
En este punto ya se diferencian con nitidez las conductas de cada modelo. El modelo aditivo con distribución de Poisson opera con futuros incrementos, el aditivo polinomial cuadrático proyecta el estado estacionario con leves incrementos y el arima la estacionariedad actual.

Es necesario aclarar que ninguno de los modelos predice el aplanamiento, lo cual no necesariamente significa que éste no vaya a ocurrir.

El siguiente cuadro muestra las proyecciones al 23 de julio, que dan lugar al gráfico anterior.

fecha	gampoisson	gampoli2	arima210
24-06-20	264316	259646	258195
25-06-20	270266	264229	261908
26-06-20	276291	268854	265687
27-06-20	282391	273519	269442
28-06-20	288566	278227	273232
29-06-20	294816	282976	277016
30-06-20	301141	287766	280821
01-07-20	307541	292598	284627
02-07-20	314016	297471	288447
03-07-20	320567	302386	292270
04-07-20	327192	307342	296102
05-07-20	333892	312340	299939
06-07-20	340668	317379	303781
07-07-20	347518	322459	307628
08-07-20	354444	327581	311479
09-07-20	361445	332745	315333
10-07-20	368520	337950	319190
11-07-20	375671	343197	323048
12-07-20	382897	348485	326907
13-07-20	390197	353814	330767
14-07-20	397573	359185	334627
15-07-20	405024	364598	338486
16-07-20	412550	370052	342344
17-07-20	420151	375547	346199
18-07-20	427827	381084	350052
19-07-20	435578	386662	353901
20-07-20	443404	392282	357747
21-07-20	451306	397944	361588
22-07-20	459282	403647	365425
23-07-20	467333	409391	369255

 

Se aprecia cómo los tres modelos consultan predicciones distintas en el tiempo, ajustándose a los criterios consignados. Claramente el arima proyecta el estado estacionario actual, lo cual constituye una posibilidad si es que el aplanamiento de la curva está lejano.

Los otros dos modelos representan efectos multiplicativos futuros, el aditivo polinomial predice incrementos muy tenues y el aditivo poisson un poco más marcados.

Escenario de peak[3]

El estudio acerca del decurso de los nuevos casos diarios es clave cuando se intenta predecir la proximidad del peak, principalmente si se toma en consideración el comportamiento de las curvas de otros países que hoy tienen aplacada y controlada la pandemia. El gráfico que sigue muestra su evolución en Chile.

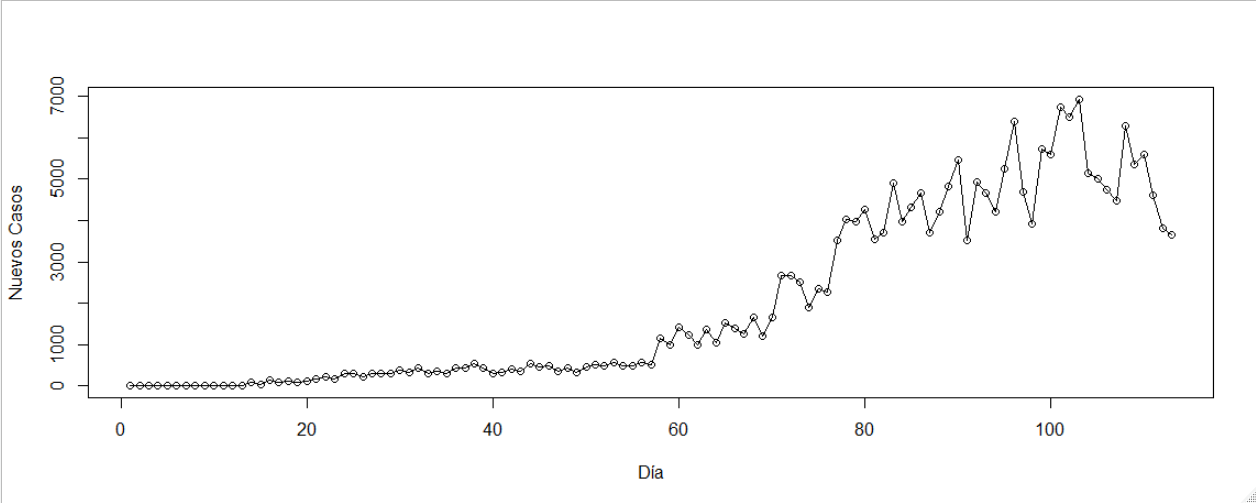
Es posible asumir la hipótesis de que habríamos ingresado al período de peak la semana pasada (del 15 al 21 de junio). Desde principios de junio, veníamos ensayando un modelo polinómico de cuarto orden, el cual predecía que Chile ingresaría a esa fase en la segunda quincena de junio.

En los días 4 y 5 de junio, las predicciones situaban su inicio en torno al 16 – 17 de junio; en los días inmediatamente siguientes, las proyecciones oscilaron entre el 13 y el 23 de junio, situándose más claramente entre los días 17 y 20. Y todas ellas indicaban que el declive comenzaría hacia fines de este mes, principios de julio.

De la observación del gráfico, se desprende que la estacionariedad queda de manifiesto precisamente en esos días. De ser así, en estos momentos nos encontraríamos en esa fase, la cual debiera durar un tiempo antes del inicio del aplanamiento.

Anexo 1: modelos ensayados

Los diversos modelos probados se sintetizan a continuación.

1. Gam Poisson con enlace raíz cuadrada

Es el modelo de mejor desempeño desde el primer minuto; logra capturar los efectos de la curva completa y sus predicciones han sido certeras en el corto, mediano y largo plazos.

2. Gam Poisson con enlace logarítmico (exponencial suavizado)

Modelo exponencial suavizado que explota, aunque menos espectacularmente que el modelo exponencial puro.

3. Quasi Poisson con enlace logarítmico

Modelo exponencial que no se comporta bien.

4. Gam Quasi con power 0.19

Se probó este modelo en las primeras semanas y el exponente surgió de calibraciones efectuadas. A pesar de funcionar bastante bien, demostró efectividad más bien de corto plazo.

5. Modelo Weibull

Se utilizó este modelo en los primeros días debido a que el comportamiento de la curva siguió una distribución de Weibull hasta fines de marzo. Su desempeño fue mediocre.

6. Quasi con enlace logarítmico

Modelo exponencial de explosión rápida.

7. Gam Quasi con enlace logarítmico

Modelo exponencial suavizado que se comporta mejor que el anterior, aunque inferior al Gam Poisson con el mismo enlace.

8. Diversos arima con combinaciones de auto rezagos y derivadas

El de mejor rendimiento, desde el comienzo ha sido el Arima  (2, 1, 0).

9. Polinomial de orden 3

De buen desempeño en el corto plazo.

10. Gam polinomial de orden 3

Buen rendimiento en el corto y mediano plazos.

11. Gam polinomial de orden 2

También de buen rendimiento en el corto y mediano plazos.

12. Modelo SIR[4]

Modelo epidemiológico simplificado, con buen comportamiento en el corto y mediano plazos.

13. Modelo mínimos cuadrados ordinarios

Modelo empleado solamente para proyectar plazos breves.

14. Se probaron algunos modelos de transferencia, incorporando la variable de población en cuarentena, pero no resultaron significativos.

Anexo 2: modelos aplicados

 

1. Gam Poisson: modelo aditivo funcional, que ajusta un modelo generalizado con distribución de Poisson (apropiada para conteos) y que utiliza la raíz cuadrada como enlace. Abarca la evolución completa desde el día uno.

Este modelo es el de mejor rendimiento desde el inicio de estos estudios. Ajusta bien, capturando las variaciones de la curva en el tiempo. Es uno de los que mejor se ha desempeñado en todas las proyecciones, desde los últimos días  de marzo, evidenciando una consistencia alta para sus predicciones de corto, mediano y largo plazo.

 

2. Gam Polinomial de orden 2: modelo aditivo que ajusta un modelo generalizado gaussiano polinomial de orden 2. Se hace cargo de toda la curva desde el día uno y su desempeño es muy bueno y regular.

 

3. Arima (2, 1, 0): serie de tiempo con dos auto rezagos y una derivada y que abarca la evolución completa desde el día uno.

Es un modelo que se ha mostrado efectivo, prediciendo con mayor cercanía que el resto, al igual que los dos anteriores, desde fines de marzo y que proyecta al corto y mediano plazo cifras consistentes día a día. Su debilidad es la sensibilidad a las variaciones de los diferenciales diarios.

 

 

 

[1] Los diversos modelos probados se consignan en el anexo 1

[2] La descripción de los modelos se encuentran en los anexos 1 y 2

[3] De acuerdo a nuestra propia definición consignada.

[4] “Evolución de las epidemias: la matemática de aislarse”, Héctor Pastén, Jorge Castillo Sepúlveda. Marzo 2020.